SHK research

Last updated October 11, 2007
Sung Ha Kang's research on Mathematical image processing: Past and current

1) Image Reconstruction: inpainting, dejittering and deblurring

(a) Image Inpainting refers to a specific image restoration task, where missing or damaged portions of an image are reconstructed. Digital image inpainting became very popular thanks to the work by Bertalmio, Sapiro, Caselles, and Ballester [ Proc. Siggraph 2000] where the authors use third order partial differential equations (PDE) to diffuse the known image information into the missing regions along the level lines. Masnou and Morel [Proc. IEEE Int'l Conf on Image Proces. 1998] drew our attention to variational models.

In Chan, Kang and Shen, we introduced the Euler's Elastica Curvature to the variational functional for higher order image inpainting. This is one of the natural ways to improve the TV inpainting method.
- Tony Chan, Sung Ha Kang and Jianhong Shen, ``Euler's Elastica and Curvature Based Inpaintings'', SIAM journal on Applied Mathematics, 63, number 2, page 564-592, 2002. (UCLA CAM 01-12)

In Kang, Chan and Soatto, we introduced Inpainting from multiple view which deals with even larger missing regions, where it is not solvable with typical local inpainting methods.
- Full details and images are at UCLA CAM02-31, ``Landmark based inpainting from Multiple view'', March 2002
- Sung Ha Kang, Tony Chan and Stefano Soatto, ``Inpainting from Multiple view'', Proceedings of first international symposium on 3D Data Processing Visualization Transmission, Pages 622-625, 2002. ( UCLA CAM 02-11 )

Chan and I investigated Error Analysis for Image Inpainting. This is the first work on error analysis for image inpainting. For general inpainting experiments, local inpainting methods work well for narrow inpainting domains, and the error bounds give analysis on this phenomenon.
- Tony F. Chan and Sung Ha Kang, `` Error Analysis for Image Inpainting'', Journal of Mathematical Imaging and Vision , Volume 26, pages 85-103, 2006. (full color images available at: UCLA CAM 04-72).

(b) Image and Video Dejittering occurs when the horizontal lines of video image frames are randomly displaced due to the corruption of synchronization signals or electromagnetic interference during video transmission.

Shen and I proposed a PDE based dejittering approach Video Dejittering by Bake and Shake. This method gives very robust numerical results and one example is shown in Figure 2.
- Sung Ha Kang and Jianhong Shen, "Video Dejittering by Bake and Shake", Image and vision computing, Volume 24, Issue 2, Pages 143-152, 2006. (Full color images available at: UCLA CAM 04-60).

Extension of this work is explored in On the Slicing Moments of BV Functions and Applications to Image Dejittering. By regularizing the moment function, this method allows to recover even a very thin lines which was impossible from previous dejittering methods.
- Sung Ha Kang and Jianhong Shen, ``On the Slicing Moments of BV Functions and Applications to Image Dejittering'', in Image Processing Based on Partial Differential Equations , Springer-Verlag, Berlin, 2007

(c) Image and deblurring is one of the classic image restoration problems and the difficulties lie on the ill-poseness of this problem. For example, typically only a blurry out of focus image, such as in Figure 3(a), is given to be deblurred to a clear and focused image.

With my Ph. D student, I proposed a blind deconvolution method, Total variation blind deconvolution using shock filters, which dramatically improves the result of blind-deconvolution.

James H. Money and Sung Ha Kang, ``Total variation semi-blind deconvolution using shock filters'', in Image and vision computing , Volume 26, Issue 2, 1 February 2008, Pages 302-314. ( IMA preprint 2106, March 2006)

2) Color Image analysis: denoising, decomposition and colorization

(a) Color Spaces and denoising: Chan, Kang and Shen, we explored various color spaces for the best color image denoising. We studied the Chromaticity-Brightness (CB) model and Hue-Saturation-Value (HSV) model, and found out it is best to treat color as one component, but independently to the brightness.

Tony. F. Chan, Sung Ha Kang and Jianhong Shen, ``Total Variation Denoising and Enhancement of Color Images Based on the CB and HSV Color Models'', Journal of Visual Communication and Image Representation, 12 : 422-435, 2001. (Full color images available at: UCLA CAM 00-25).

(b) Color image decomposition: With Aujol, I have consider color image decomposition in Color Image Decomposition and Restoration. This is one of the first work on color texture analysis.

Jean-Francois Aujol and Sung Ha Kang, ''Color Image Decomposition and Restoration'', Journal of Visual Communication and Image Representation , Volume 17, Number 4, pages 916-928 2006. (Full color images available at: UCLA CAM 04-73.)

(c) Colorization refers to an image processing task which recovers color of gray scale images when only small regions with color are given. In Variational Models for Image Colorization via Chromaticity and Brightness Decomposition, we proposed and analyzed couple of variational models for colorization. Figure 4. shows an example of texture colorization using image decomposition techniques.

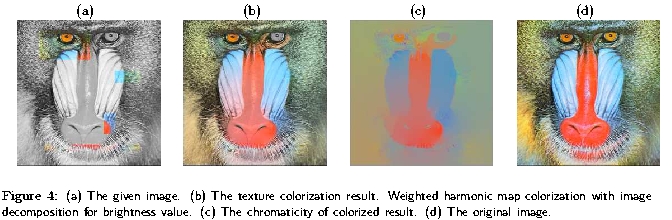
Sung Ha Kang and Riccardo March, ``Variational Models for Image Colorization via Chromaticity and Brightness Decomposition'', IEEE transaction in Image Processing, Volume 16, Number 9, Pages 2251-2261, 2007 (Full color images available at : IMA preprint 2138, October 2006)

3) Image segmentation and Quantization
Image Segmentation is a classical problem in image processing. From Geman and Geman's mixture random-field models [IEEE PAMI 1984] to Mumford and Shah's piecewise smooth variational image models [Comm. Pure Appl. Math. 1989], segmentation has been extensively studied by various researchers. One of the most influential methods is the level-set approach by Chan and Vese [IEEE Trans. Image Proc. 2001].

Multiphase Image Segmentation: Jung, Shen and I, in Multiphase Image Segmentation via Modica-Mortola Phase transition, proposed a novel multiphase segmentation model. This procedure is truly a multi-phase segmentation by construction of the model, which represents each segment by an integer, and an elegant way to solve true multi-phase segmentation problem.
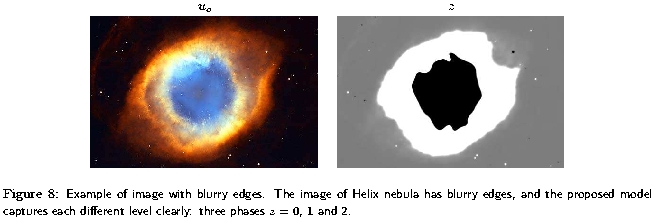
- Yoon Mo Jung, Sung Ha Kang and Jianhong Shen, ``Multiphase Image Segmentation via Modica-Mortola Phase transition'', SIAM applied Mathematics , Volume 67, Issue 5, Pages 1213- 1232, 2007. (Full color preprint available at UCLA CAM06-31, and IMA preprint 2124, June 2006)

Image quantization: In Quantum TV and Applications in Image Processing, we explored the computational aspect of the celebrated TV model. This is discrete version of total variation minimizing computation using stochastic/Markovian gradient descent method. Figure 5, we demonstrate the quantization performance of the free quantum TV model with five levels.
- Jianhong Shen and Sung Ha Kang, ``Quantum TV and Applications in Image Processing'', Volume 1, Number 3, Pages 557-575, 2007 (preprint UCLA CAM07-09 )